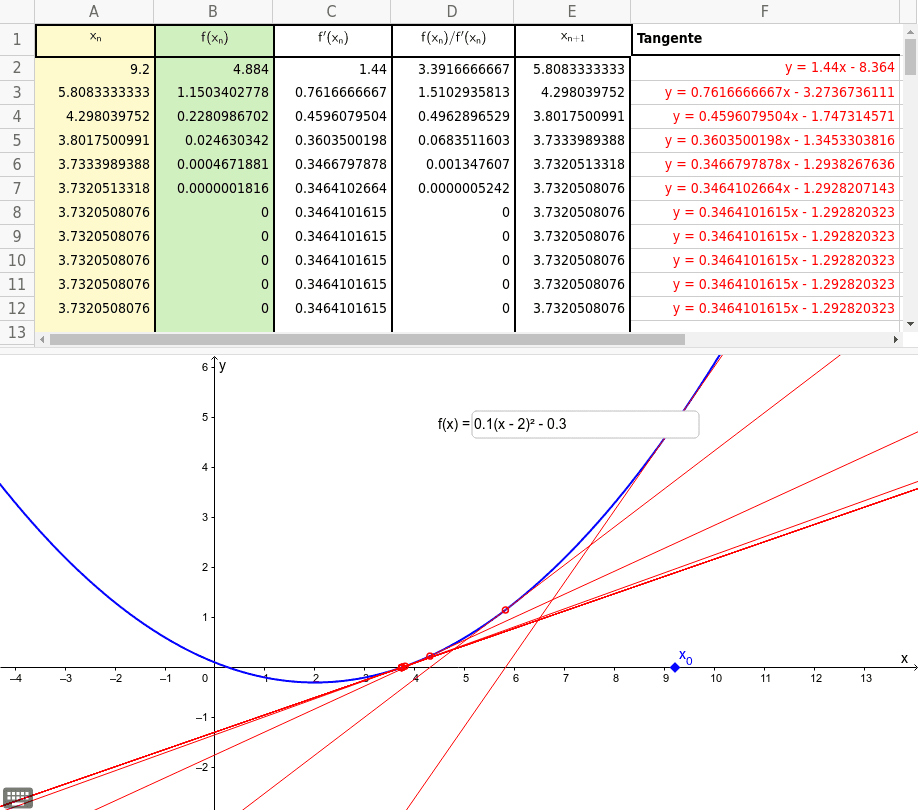
Jacobi Verfahren Beispiel | Benannt ist es nach carl gustav jacob jacobi. Man bezeichnet das verfahren (1) als konvergent, falls für alle startvektoren x(0) die folge x(k) gegen die exakte lösung x konvergiert. Als einf uhrung in die idee eines iterativen verfahrens bietet sich etwa das heronsche verfahren zur wurzelberechnung an. Es gilt (i ca)= (i d 1 1 a 1) =max fj 1 4 h 2 j j eigenwert von a 1 g =1 2sin 2 (1 2 h)=cos( h) 1 1 2 2 h 2: Praktikabel wurde das verfahren mit dem aufkommen von computern.
Benannt ist es nach carl gustav jacob jacobi. Wir schreiben x1 = (b1 a12x2 a13x3)=a11 x2 = (b2 a21x1 a23x3)=a22 x3 = (b3 a31x1 a32x2)=a33: Orthogonales komplement i suchen neues eigenpaar (λ, x), das nah bei (θ, y) liegt i betrachten orthogonale zerlegung x = y +v mit v ∈ y ⊥ x ∈ cn = span(y)⊕y⊥ i liefert eigenproblem: Die numerik einführung besteht aus den folgenden videoreihen: Wir definieren eine matrix mit den gleichen diagonalelementen wie und null in allen nichtdiagonalelementen.

Im beispiel werden die iterativen löser. Orthogonales komplement i suchen neues eigenpaar (λ, x), das nah bei (θ, y) liegt i betrachten orthogonale zerlegung x = y +v mit v ∈ y ⊥ x ∈ cn = span(y)⊕y⊥ i liefert eigenproblem: Ein sehr ahnliches verfahren entwickelte carl gustav jacobi 1845. Das skript hat seinen ursprung in einer vorlesung ¨uber numerische behandlung von Entwickelt wurde das verfahren, da das gaußsche eliminationsverfahren zwar eine exakte lösungsvorschrift darstellt, sich jedoch für rechenfehler sehr anfällig zeigt. Betrachtet werden, welche eine transformation der kartesischen in die kugelkoordinaten beschreibt. Praktikabel wurde das verfahren mit dem aufkommen von computern. Ausgangspunkt ist die bilineare form mit der folgenden fragestellung: Import netgen.geom2d as geom2d from ngsolve import * from ngsolve.webgui import draw 3: Man bezeichnet das verfahren (1) als konvergent, falls für alle startvektoren x(0) die folge x(k) gegen die exakte lösung x konvergiert. Die partiellen ableitungen der einzelnen komponenten lauten: Import numpy as np import scipy.sparse as sp import matplotlib.pyplot as plt. Allerdings ist es deutlich langsamer als das im
Das di usionsproblem mit der matrix a 1. Wir definieren eine matrix mit den gleichen diagonalelementen wie und null in allen nichtdiagonalelementen. A = b+(a−b), b ∈ c n× somit ist das lgs ¨aquivalent zu: • falls a irreduzibel diagonaldominant ist, gilt. Wir geben die wichtigsten beispiele f ur die aufspaltungen a = p n.
2d geometrie¶ eine klassische geometrie für numerische versuche ist der sogennante l. Gegeben ist die symmetrische matrix a, gesucht ist eine orthogonale. Fu r die asymptotische konvergenzrate gilt somit ln( (i k d 1 a 1)) ln(1 1 2 2 h 2) 1 2 2 h: Das di usionsproblem mit der matrix a 1. Praktikabel wurde das verfahren mit dem aufkommen von computern. Orthogonales komplement i suchen neues eigenpaar (λ, x), das nah bei (θ, y) liegt i betrachten orthogonale zerlegung x = y +v mit v ∈ y ⊥ x ∈ cn = span(y)⊕y⊥ i liefert eigenproblem: Wir definieren eine matrix mit den gleichen diagonalelementen wie und null in allen nichtdiagonalelementen. Ein sehr ahnliches verfahren entwickelte carl gustav jacobi 1845. Ausgangspunkt ist die bilineare form mit der folgenden fragestellung: Hierbei wird vorausgesetzt, dass der begri eines iterativen verfahrens bereits bekannt ist. X = − 2 10 − 1 10y + 1 10z y = 1 8 + 1 8x − 1 8z z = − 3 20 + 1 20x − 1 20y Die partiellen ableitungen der einzelnen komponenten lauten: Gibt beispiele, in denen erstere konvergiert und letzteres divergiert, und umgekehrt.
Betrachtet werden, welche eine transformation der kartesischen in die kugelkoordinaten beschreibt. Orthogonales komplement i suchen neues eigenpaar (λ, x), das nah bei (θ, y) liegt i betrachten orthogonale zerlegung x = y +v mit v ∈ y ⊥ x ∈ cn = span(y)⊕y⊥ i liefert eigenproblem: Praktikabel wurde das verfahren mit dem aufkommen von computern. Wir definieren eine matrix mit den gleichen diagonalelementen wie und null in allen nichtdiagonalelementen. Es gilt (i ca)= (i d 1 1 a 1) =max fj 1 4 h 2 j j eigenwert von a 1 g =1 2sin 2 (1 2 h)=cos( h) 1 1 2 2 h 2:
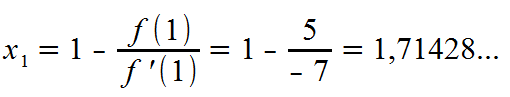
Import netgen.geom2d as geom2d from ngsolve import * from ngsolve.webgui import draw 3: Diagonalmatrix) mit dem ziel, das matrizeneigenwertproblem zu lösen. • falls a irreduzibel diagonaldominant ist, gilt. Entwickelt wurde das verfahren, da das gaußsche eliminationsverfahren zwar eine exakte lösungsvorschrift darstellt, sich jedoch für rechenfehler sehr anfällig zeigt. Das skript hat seinen ursprung in einer vorlesung ¨uber numerische behandlung von X = − 2 10 − 1 10y + 1 10z y = 1 8 + 1 8x − 1 8z z = − 3 20 + 1 20x − 1 20y Iterationsschritt 0 1 2 3 x 1 0 1;67 1;22 1;07 x 2 0 0;67 0;89 0;96 x 3 0 0;67 0;89 0;96 Allerdings ist es deutlich langsamer als das im Praktikabel wurde das verfahren mit dem aufkommen von computern. Man bezeichnet das verfahren (1) als konvergent, falls für alle startvektoren x(0) die folge x(k) gegen die exakte lösung x konvergiert. A = b+(a−b), b ∈ c n× somit ist das lgs ¨aquivalent zu: Orthogonales komplement i suchen neues eigenpaar (λ, x), das nah bei (θ, y) liegt i betrachten orthogonale zerlegung x = y +v mit v ∈ y ⊥ x ∈ cn = span(y)⊕y⊥ i liefert eigenproblem: A(y +v) = λ(y +v) i verwenden projektion von a in y⊥:
Jacobi Verfahren Beispiel: Praktikabel wurde das verfahren mit dem aufkommen von computern.
0 komentar: